Drawing on History
Benjamin Senson Madison College/ MMSD Planetarium
Welcome to the AAS Education Blog! This post is part of a biweekly series of blog posts from astronomers and educators in the extended AAS community, curated by the AAS Education Committee. Subscribe here (choose the "AASeducation" list) to receive future posts directly into your inbox; also follow us on Twitter. We welcome feedback and topic suggestions, as well as guest article submissions! —eds.
Science is often perceived as a grand rise from ignorance toward understanding. The daily practice of a research scientist focuses on challenging the assumptions of a model or theory so as to reveal its limitations and failures. This approach can be incorporated into astronomy instruction at the introductory level. In this article, I explore a method of drawing the universe through the lens of a specific model of the cosmos (i.e., Ptolemaic, Copernican). Physically drawing out a system to demonstrate its ability to produce an observation, such as retrograde motion, and to demand that it can produce a horizon view of the sky as it is seen in a moment, challenges a student's understanding of vocabulary, concepts, and practical application of the elements of a model. It also transforms the approach to scientific work as an endeavor to challenge current understandings to "save the appearances" into a practical and personal experience for the student. This approach, inspired originally by Michael Zeilik, has been expanded to allow for a wide range of students to engage with the approach and to allow it to engage students directly with the mechanisms of the universe, especially when they turned out to be incorrect.
In Interactive Lesson Guide for Astronomy, Michael Zeilik gave the following description of the possible positions of various planets in the sky:
It is just after sunset. Mars is rising in the east. Venus is at maximum eastern elongation, 45 degrees from the Sun. Jupiter is due south, halfway between the Sun and Mars in angular distance.
Zeilik’s expectation was that by translating these descriptions into angular positions, a student would be able to plot onto two charts their required positions for both a heliocentric and a geocentric model of the Cosmos, and thus see how this one set of appearances can have at least two possible ways in which they are produced.
This was the trigger for my predecessor, Art Camosy, to create a series of these “Zeilik problems” for our high school students as they faced the full scope of astronomical history and each of the major cosmological models of Thales, Pythagoras, Aristotle, Callippus, Eudoxus, Plato, Ptolemy, Copernicus, Tycho, and Galileo. They needed to confront the challenge taken from Plato as expressed through Simplicius in the sixth century,
Plato lays down the principle that the heavenly bodies’ motion is circular, uniform, and constantly regular. Thereupon he sets the mathematicians the following problem: what circular motions, uniform and perfectly regular, are to be admitted as hypotheses so that it might be possible to save the appearances presented by the planets? (Duhem, To Save the Phenomena, 5)
This problem of the description of the positions of the planets at an instant in time as the appearances to be saved, then by necessity demands that the drawings a student creates must be able to cause them to appear.
Taught in a planetarium, students in my high school course experience ~40 days of “going dark” during which they are exposed to the unaided observational appearances that are the evidence available to support, or attack, any given cosmological model. In the remainder of the course, they are engaged with the models of the ancient Greeks from Thales, and Ptolemy, to the breakthroughs of Copernicus, Brahe, Galileo, Kepler, and Newton. They are exposed to the brilliance of models in their own times before exploring each model’s ultimate collapse when exposed to new ideas and technologies during the remainder of the course.
In my college setting, with no planetarium access, the same challenge is present, how can they extend their comprehension of a model and develop some skill in applying their knowledge about a model of the heavens to solving a specific problem? This makes it clear that the planetarium, while an amazing tool for teaching, is not the critical component for developing this competency. Exposure to the visual experience of the dynamic sky, diagrams and discussions of the essential components of each model, and guided discovery of their observational outcomes is not enough to ensure that students develop a complete and robust understanding of each model.
The experiences described in this article were created to develop such an understanding by ensuring that every student was personally challenged to create representations of each model and thus see how each can lead to the same observational appearances. Conceptual lessons without application are like tourism without travel (an impossibility), for developing the essential skills of a scientist. We can create seeds of understanding that lead to scientific literacy and conceptual understanding, but they don’t often go far enough to reveal the limitations of knowledge as starkly as does exposure to the necessity of producing a specific outcome, to “save the appearances.”
This pedagogical challenge of transforming learning experiences into personal engagement with a problem has been the focal point for continuous reflection on how to adapt this general approach of drawing the cosmos for developing a deeper, more detailed, understanding of a given model as well as providing the differentiation of the challenge so that a similar learning outcome can be achieved across the wide range of student’s depth of knowledge and skills in a typical introductory astronomy classroom setting.
I inherited a set of Ptolemaic and Copernican experiences from Art Camosy that each contained the following elements: 1) They demonstrated how a system produces a retrograde motion; 2) They showed how that retrograde motion is determined by a variable such as the sidereal period of the deferent of the superior planet; and 3) They presented students with a Zeilik-inspired horizon problem for the model.
In Figure 1, you can see how the Ptolemaic model and its deferent and epicyclic motion for a superior planet produces very different sizes and separations of the observed retrograde loops simply by varying the sidereal period of this theoretical planet from 36 to 60 months. This can then be used to analyze the variation in the planet’s observed speed. As a simplification, the drawing of one system with a slower speed and completely separate drawing at the higher speed allows insight into the much deeper and more challenging visualization of the impact of an eccentric and its outcome of a regularly varying rate of apparent motion on the retrograde loops actually seen in the full models of the universe.
Given the evidence for how retrograde motion can be produced in a model, the related horizon problem starts with only a Zeilik-style description of a moment in time in a “real sky.” The student’s task is then to create the drawings for this situation as a true horizon diagram as well as a 2D interpretation of this simplified model of the cosmos.

Interpreting a description of positions in the sky into a horizon and 2D model drawing challenges the student's mind and forces the emergence of an application-level understanding of the terminology and mechanisms associated with the model. It also reveals immediately whether or not they have an application level of understanding of the underlying restrictions and limitations of the model implemented, e.g., for a Ptolemaic model, the necessity of a full plenum universe with no overlaps or voids, and the bound and the parallel rules for epicycles.
My development of these activities has taken them to become more differentiated across a wider range of students with “Zeilik” problems that are significantly more challenging due to the way in which the appearances of each planet in the sky are described. For example, the position of Mercury could be described as being at greatest western elongation versus being 14 days after inferior conjunction. The process of producing the drawings is the same, but the change in description changes the cognitive rigor of the task and requires understanding the model on a deeper level with the application of knowledge about the sidereal, synodic, or angular rates of motion for a given object, for example.
Finally, as shown in Figure 2, this same approach has been extended to begin to visualize the necessity for specific ratios in the sizes of the components of a single model. In order to save the appearances of the degree to which Mercury and Venus are bound to the Sun, the deferent of Mercury must be at a specific relative size to that of Venus. Figuring out that ratio is already done for the students allowing them to see their impact without the additional mathematical challenges. If we were to take an image of this final product, it could be shown at both larger and smaller absolute sizes which reveals the necessity, separately from the mechanism for producing the pattern in planetary motion, for the additional work to determine the absolute size of a single element within the model. In totality, this sequence of experiences, repeated for at least two models of the universe, creates an opportunity for the student to see how the development of these models is not just toward a scale model, but to be complete they also need to be one with known relative size if they are to represent the “real” cosmos, as known at that time.
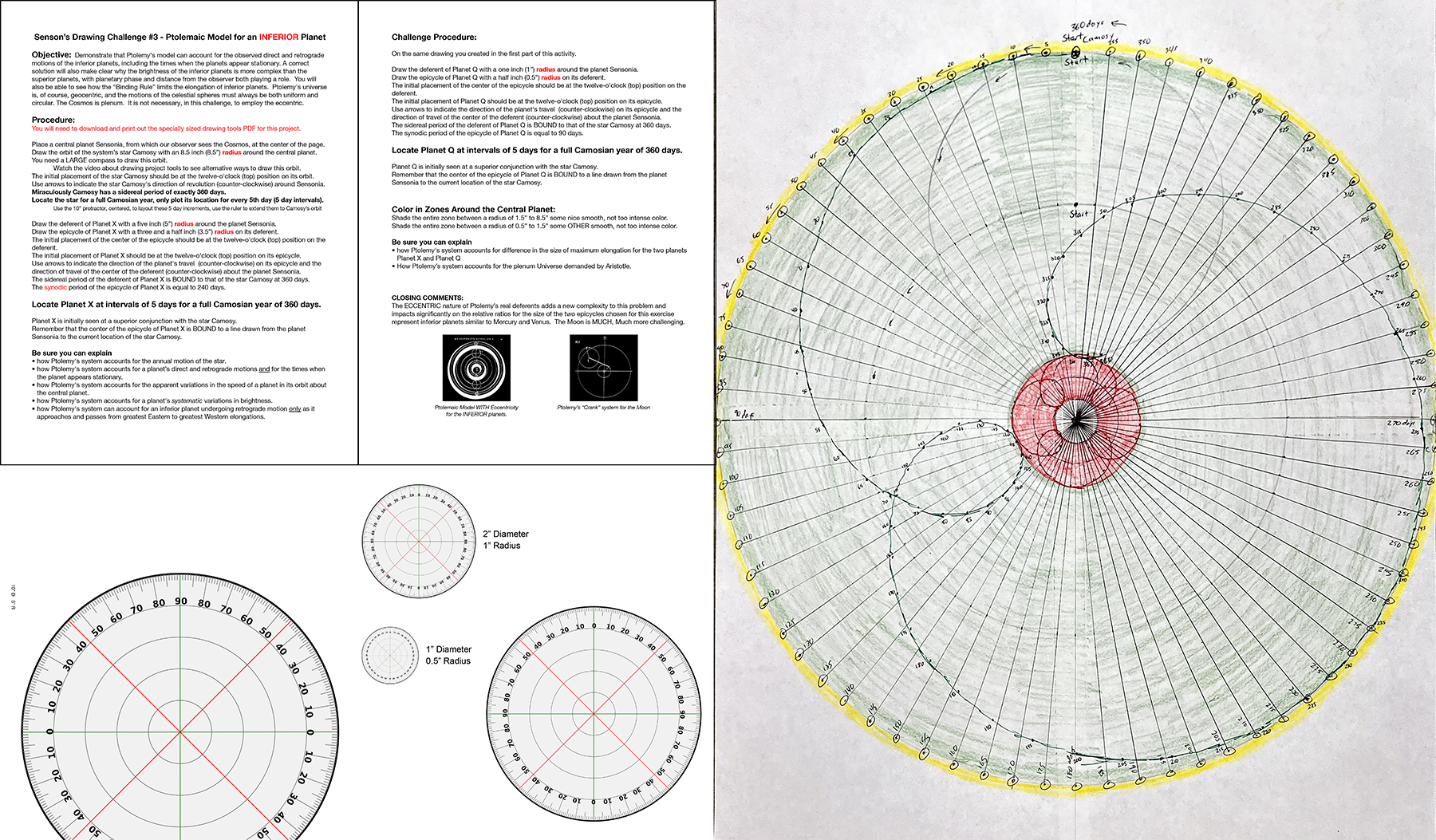
The challenge of drawing on history to draw a model of the universe is a powerful and personal experience for students. A challenge can be completed in 50-90 minutes for students that have the prior preparation work done to develop a conceptual understanding of new and unique vocabulary and/or mechanisms in a given model.
Ultimately, the real power of these exercises, and the structure for my course, is the revelation that many models can produce the observed positions of planets in the sky. Scientists seek evidence that can be used to reveal the limitations and failures of a model and thus push us forward toward a deeper and more useful understanding of the cosmos in which we live. By seeking to destroy the underpinnings of a model, we strengthen it every time we fail to do so.
For anyone interested in using this method in your instruction, please contact the author at [email protected] to request access to documents.
References:
Zeilik, M. (2001). Interactive Lesson Guide for Astronomy: Cooperative Learning Activities. Learning Zone.
Duhem, Pierre (1969). To Save the Phenomena, An Essay on the Idea of Physical Theory from Plato to Galileo. Chicago: University of Chicago Press.

