This Month in Astronomical History: June

Each month as part of this series from the AAS Historical Astronomy Division (HAD), an important discovery or memorable event in the history of astronomy will be highlighted. This month's guest author, Jason E. Ybarra (Bridgewater College), focuses on the Greek astronomer Eratosthenes and his renowned calculation of the circumference of the Earth. Interested in writing a short (500-word) column? Instructions along wth previous history columns are available on the HAD webpage.

Eratosthenes and the Circumference of the Earth

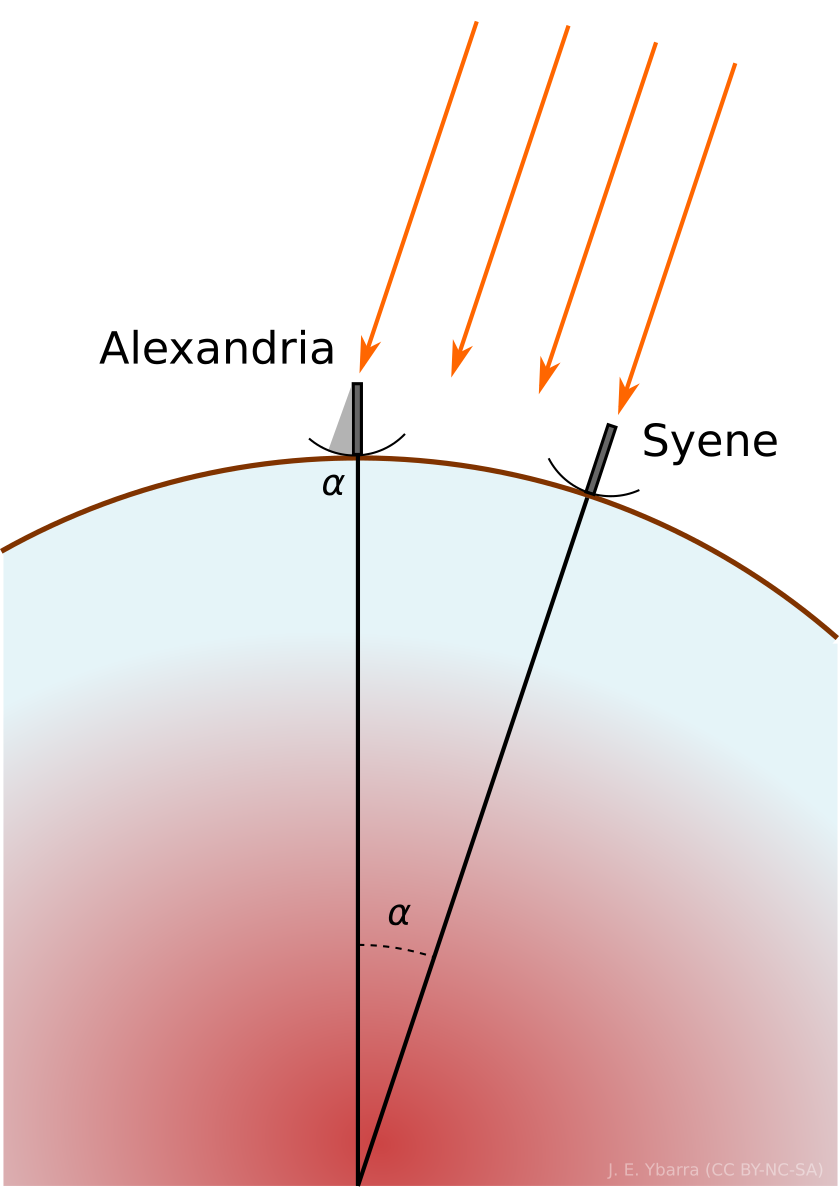
In the northern hemisphere, the June solstice signifies the longest day of the year, during which the Sun reaches its highest point in the sky. On this day at local noon, the Sun appears directly overhead to an observer on the Tropic of Cancer. It was on this fact, which occurred annually near the Egyptian city of Syene, that the Greek astronomer Eratosthenes (c. 276 – c.194 BCE) based his renowned calculation of the circumference of the Earth. This accomplishment came about from the convergence of Greek science and Egyptian land surveying. 

Most of Eratosthenes’ works were lost during the destruction of the Library of Alexandria; however we know of Eratosthenes’s method from the Greek astronomer Cleomedes. In his treatise on astronomy (Meteōra, I.7), Cleomedes recorded that Eratosthenes measured the circumference of the Earth using Euclidean geometry with the following assumptions: 

...first...that Syene and Alexandria are located below the same meridian; [second] that the distance between the two cities is 5,000 stades. Third, [assume] that the rays sent down from different parts of the Sun to different parts of the Earth are parallel, as geometers assume to be the case.¹ 

While a gnomon* at Syene produced no discernable shadow during the summer solstice, a gnomon at Alexandria produced a shadow that Eratosthenes measured to be an arc of 1/50th of a circle (Fig. 1). This resulted in the calculation of Earth’s circumference to be 250,000 stades^†. However, the length of a stade is uncertain. According to the Greek historian Herodotus (c. 484 – c. 425/413 BCE), a stade is equivalent to 600 Greek feet. Still, there are at least three different variations of a Greek foot. The most commonly accepted value of a stade is 184.8 meters, giving a circumference of 46,000 km (29,000 miles), about 15% off from the modern value.² 

As director of the Library of Alexandria, Eratosthenes no doubt learned that in the town of Syene a gnomon casts no shadow on the June solstice. The location of Syene was fortuitous, at the southernmost end of ancient Egypt and near the Tropic of Cancer. On the other hand, the city of Alexandria was near the northern end of Egypt. According to the Greek historian Strabo (c. 64 BCE – c. 24 CE), 

In Egypt, the Nile passes in a straight line from the little cataract above Syene and Elephantine, at the boundary of Egypt and Ethiopia, to the sea.... the Nile takes away and adds soil, and changes conformations of land, and in general hides from view the signs by which one’s own land is distinguished from that of another. Of necessity, therefore, the lands must be re-measured again and again. And here it was, they say, that the science of land-measuring originated.³ 

Thus, it has been argued that the arc between Alexandria and Syene would have been one of the best measured available to Eratosthenes, allowing him to accomplish this remarkable task of measuring Earth’s circumference. 

* The gnomon is the component of a sundial that produces a shadow. For a Greek scaphe sundial at the time of Eratosthenes the gnomon would be a vertical stick (see Fig. 2).

† Other Greek sources list Eratosthenes’s value as 252,000 stades. For more information regarding the two values see Carman & Evans (2015, “The Two Earths of Eratosthenes,” Isis, 106, 1) 

Figures

Fig. 1. Illustration of the geometrical arrangement used by Eratosthenes to measure the circumference of the Earth (CC BY-SA 3.0). 

Fig. 2. Greek scaphe sundial at the Clemens Sels Museum Neuss. Image credit: Hartmann Linge (CC BY-SA 3.0). 

References 

1. Cleomedes & Todd, R. B., & Bowen, A. C. 2004, Cleomedes' Lectures on Astronomy: A Translation of The Heavens, (Berkeley, CA: Univ. of California Press) 

2. Walkup, N. 2010, “Eratosthenes and the Mystery of the Stades — How Long is a Stade?” Convergence, https://www.maa.org/press/periodicals/convergence/eratosthenes-and-the-mystery-of-the-stades-how-long-is-a-stade 

3. Fischer, I. 1975, “Another Look at Eratosthenes’ and Posidonius’ Determinations of the Earth’s Circumference,” QJRAS, 16, 152