This Month in Astronomical History: February

Each month as part of this series from the AAS Historical Astronomy Division, an important discovery or memorable event in the history of astronomy will be highlighted. This month's guest author Jason E. Ybarra (Bridgewater College) focuses on the 400th anniversary of Kepler's third (or harmonic) law of planetary motion. Interested in writing a short (500 word) column? Instructions along wth previous history columns are available on the HAD webpage.

400 Years of Kepler’s Third Law

This year is the 400th anniversary of Kepler’s third (or harmonic) law of planetary motion. In February 1619, Johannes Kepler’s five-volume Harmonices Mundi was typeset and readied for printing. In book five, Kepler addressed planetary motions and tied these motions to musical harmonies. Reflecting the thought and culture of the time, this book was a hybrid of old world mysticism and the emergence of scientific thought.¹

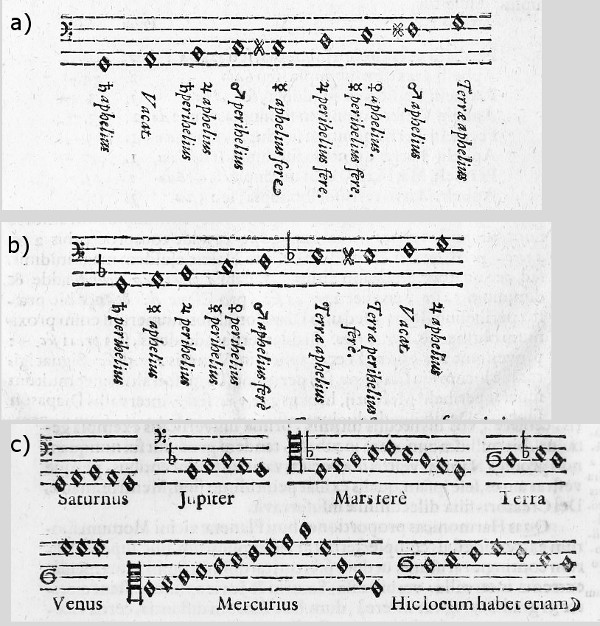
Twenty-four years earlier, in 1595, Kepler postulated that the ratios of distances between the Sun and the planets, and the number of planets, were set by the Creator according to geometric principles. He considered the set of five regular polyhedra, known as the Platonic Solids, and attempted to fit them within the orbits of the six known planets (Fig. 1). However, the fit was far from perfect, and he was only able to approximate the orbital sizes. Kepler needed something more, and over the next twenty years developed a harmonic model based on music intervals (Fig 2).²

In book five of Harmonices Mundi, Kepler maintains that the polyhedral hypothesis sets the basic structure of the solar system, while the motions and eccentricities of the planets are set by musical harmony.³ In chapter three, he discusses the motions of the planets, setting the groundwork for his musical harmonic hypothesis. The hidden gem within is Kepler’s harmonic law, the relationship between the sizes and periods of the planetary orbits (Fig. 3). Kepler reveals that this discovery was made soon after sending the books to the printer, writing:

…It was conceived mentally on the 8th [of] March in this year one thousand six hundred and eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labor of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialterate^† proportion of their mean distances…⁴

Kepler’s discovery had two profound effects. First, it provided another nail in the coffin for the Ptolemaic geocentric model. By placing the Sun at the center of the Universe, Copernicus showed that relative distance between the Sun and the planets could be geometrically determined from observations. Secondly, perhaps even more importantly, it had predictive potential.¹ In book four of Kepler’s Epitome, published a year later, he applies the harmonic law to the motions of the Galilean moons.

Of the contents of Kepler’s Harmonices Mundi, only the harmonic law endured. Sixty-eight years after the publication of Harmonices Mundi, Isaac Newton published his three-volume Principia Mathematica containing the foundations of classical mechanics. In book three of Principia, De mundi systemate, Newton showed that Kepler's harmonic law, along with Kepler’s other two laws of motion, are a consequence of his Law of Universal Gravitation.

Sesquialterate^† meaning 3/2th power

Figures

Figure 1. Kepler’s Polyhedra Law from Harmonices mundi libri V. (From the volume held by the Smithsonian Libraries/Dibner Library of the History of Science and Technology)

Figure 2. Figures from Harmonices mundi libri V pages 204 [a & b] and 207 [c] (From the volume held by the Smithsonian Libraries/Dibner Library of the History of Science and Technology)

Figure 3. Kepler’s harmonic law in section VIII, Chapter III of Harmonices mundi libri V. (From the volume held by the Smithsonian Libraries/Dibner Library of the History of Science and Technology)

References

1.  Love, D. K. 2015, Kepler and the Universe: How One Man Revolutionized Astronomy (Amherst, NY: Prometheus Books)

2.  Gingras, B. 2003, Johannes Kepler's Harmonice mundi: A "Scientific" version of the Harmony of the Spheres, JRASC, 97, 228

3.  Brackenridge, J. B. 1982, Kepler, elliptical orbits, and celestial circularity: A study in the persistence of metaphysical commitment: Part II, AnSci, 39, 265

4.  Kepler, J., Aiton, E. J., Duncan, A. M. & Field, J. V. 1997, The Harmony of the World (Philadelphia, PA: American Philosophical Society)